Difference between revisions of "Warangps"
| Line 44: | Line 44: | ||
(1D, 2D or 3D) and on the signal properties (correlated or not? two or more plane waves?). One common way to look on this | (1D, 2D or 3D) and on the signal properties (correlated or not? two or more plane waves?). One common way to look on this | ||
problem is to view the superposition of two harmonic plane waves and explore at what minimum distance the peaks of the | problem is to view the superposition of two harmonic plane waves and explore at what minimum distance the peaks of the | ||
| − | two plane waves will merge to a single maximum in the wavenumber plane. The graphical tool [[Gpfksimulator|gpfksimulator]] allows | + | two plane waves will merge to a single maximum in the wavenumber plane. The simple answer can be understood by assuming that |
| + | the array response functions for each individual plane wave just add together. Then it becomes clear that as soon as two | ||
| + | plane waves are separated from each other in the wavenumber domain by less than the width of the main lobe width, the two | ||
| + | peaks can not be resolved any more. The width of the main lobe peak in the array response function is called <math>k_{min}</math> | ||
| + | and is related approximately to the overall array aperture by | ||
| + | |||
| + | <math> | ||
| + | k_{min} = \frac{2\pi}{D_{max}} | ||
| + | </math> | ||
| + | |||
| + | The graphical tool [[Gpfksimulator|gpfksimulator]] allows | ||
you to do so and explore by yourself the problem of [[Multiple plane wave arrivals|multiple plane wave arrivals]]. | you to do so and explore by yourself the problem of [[Multiple plane wave arrivals|multiple plane wave arrivals]]. | ||
Given ''just'' two not-correlated (outphased) plane wave arrivals | Given ''just'' two not-correlated (outphased) plane wave arrivals | ||
Revision as of 10:00, 11 March 2010
Contents
- 1 Warangps - Overview
- 2 Loading coordinates
- 3 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}}
- 4 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{max}}
- 5 Typical usage
Warangps - Overview
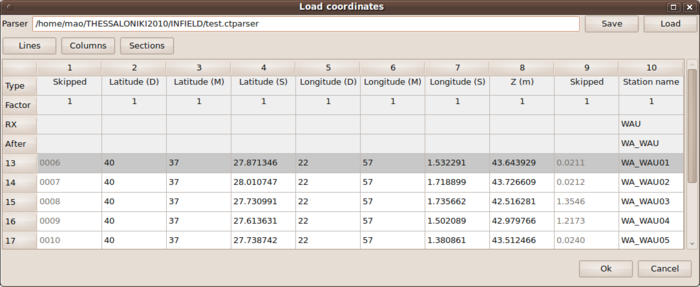
Warangps is a graphical tool for displaying the status and coordinates of gps devices in a distributed sensor network. Among other things (to be described later), warangps can be used to display the array response function for a specific array geometry.
Loading coordinates
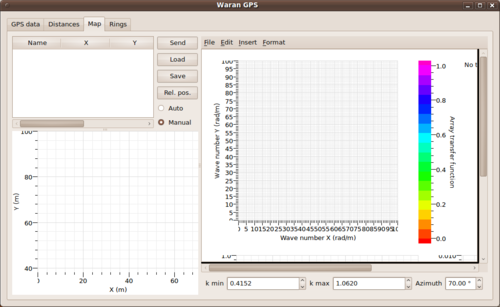
After starting up warangps, you should switch to the Map tab of the graphical user interface and set the radio button from Auto to Manual. Only then you are able to push the Load button to open a free format ASCII coordinate file.
After locating an appropriate file with the file browser, a file parser window will be opened. The flexibel parser is described in detail in the multi-column parser page. Here we provide an example coordinate file and a corresponding parser file.
After loading the pre-configured parser file or after specifying the different column entries by yourself for your own coordinate file, you will load the coordinates by confirming with the Ok button.
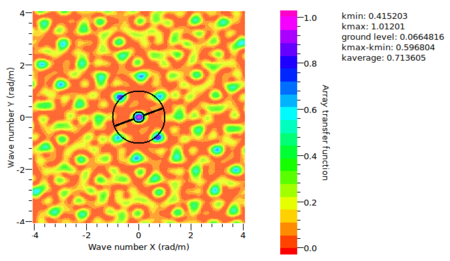
The displays in warangps will change immediately presenting the coordinates in a table (upper left) and on a map (lower left). The array response function (ARF) for the corresponding array geometry will be computed in the wavenumber domain and is displayed in the right drawing area of warangps. On top of the wavenumber map, two circles are drawn for automatically determined values of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{max}} . Details about the meaning of those quantities and the automatic computation from the array geometry are given below in the corresponding sections.
Besides the ARF, there are two more useful visualizations derived from the array response function:
- Directly below the ARF figure, 1-D cross sections along different look directions for the wave propagation are plotted. The grey lines in the background show cross sections in all directions in 2 degree steps. The black curve displays a cross section along the direction chosen in the Azimuth spin box located on the right below the drawing area. The black curve is only drawn in between the two circles for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{max}} .
- On the lower right of the drawing area, you will find a display of 4 distinct wavenumber values, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}/2} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}} , Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle k_{max}/2} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{max}} , as curves in frequency vs. slowness which finally provide information on the capabilities of the array geometry in terms of resolution and expected aliasing features (see below Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{max}} ). The intention of this plot is to export the layer of this curve that can then be overlaid to the display of f-k analysis results in max2curve.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min}} is used to quantify the resolution capabilities of a specific array geometry. The definitionis based on the following idea: Given two signals propagating with similar wavenumbers, what is the minimum distance between wavenumbers that will still allow to find two separated peaks in the wavenumber map?
You will most probably find several answers to this question depending on the dimensionality of the array configuration (1D, 2D or 3D) and on the signal properties (correlated or not? two or more plane waves?). One common way to look on this problem is to view the superposition of two harmonic plane waves and explore at what minimum distance the peaks of the two plane waves will merge to a single maximum in the wavenumber plane. The simple answer can be understood by assuming that the array response functions for each individual plane wave just add together. Then it becomes clear that as soon as two plane waves are separated from each other in the wavenumber domain by less than the width of the main lobe width, the two peaks can not be resolved any more. The width of the main lobe peak in the array response function is called and is related approximately to the overall array aperture by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{min} = \frac{2\pi}{D_{max}} }
The graphical tool gpfksimulator allows you to do so and explore by yourself the problem of multiple plane wave arrivals. Given just two not-correlated (outphased) plane wave arrivals